Valor RMS
El valor RMS (Root Mean Square), valor cuadrático medio o valor eficaz se puede entender como el valor de tensión que producirá una disipación calorífica en una resistencia óhmica cuando fluye una corriente a través de esta, de forma equivalente a lo que produciría un valor en corriente continua (CC); es decir, este valor se considera como un valor constante a partir de una onda variable, lo cual simplifica los cálculos y permite hacer mediciones. Si bien es usado típicamente para formas de onda periódicas, también puede ser aplicado a cualquier forma de onda, sean estas constantes o no.
De acuerdo a su nombre, el valor RMS es la raíz cuadrada del promedio de los cuadrados de los valores instantáneos de la forma de onda, pudiendo establecerse a partir del voltaje RMS o Vrms.
Al valor RMS se le suele denominar "valor efectivo" (generalmente se representa con Veff), cuando el valor de la tensión RMS de una forma de onda sinusoidal alterna se usa para comparar la potencia eléctrica que se entrega a una carga determinada, desde un circuito DC equivalente.
Como ejemplo, en la red eléctrica de algunos países de europa se utilizan 220 VAC, esto indica un valor efectivo de "220 Voltios RMS", lo cual implica que la tensión RMS sinusoidal de las tomas de corriente son capaces de entregar la misma potencia media positiva, tal como lo harían 220 Voltios de tensión de CC constantes, tal y como se muestra a continuación:
Por lo tanto, de forma equivalente el voltaje DC que generaría la misma potencia sería:
Cálculo del valor RMS de una onda sinusoidal
De manera intuitiva se podría pensar que el promedio de los valores instantáneos de la forma de onda sinuosidal nos dan el valor rms; sin embargo, como ya se mencionó anteriormente, de acuerdo a sus siglas el valor rms no se calcula directamente como un valor promedio de la forma de onda sinusoidal, de lo contrario la parte positiva y la parte negativa en un ciclo de la onda se anularían, es decir, obtendríamos un valor promedio igual a cero, con lo cual la potencia obtenida también sería cero.
Para obtener el valor RMS de una onda sinusoidal, podemos hacer uso de dos métodos: El método analítico y el método gráfico.
Método analítico
Matemáticamente se puede calcular el valor del voltaje o corriente rms de una forma de onda periódica usando la expresión siguiente:
Entonces, para una onda con comportamiento periódico sinosuidal que se define a partir de la función f(t):
y usando la expresión de la definición anterior para hallar el Voltaje rms, se tiene:
Luego, por la identidad trigonométrica del ángulo doble:
Además, al realizar y evaluar la integración a través de los límites tomados para un período "T" o de 0° a 360° y donde, ω=2π/T, se obtiene:
Por lo que la expresión resultante es:
Finalmente, se demuestra que para una onda sinusoidal, el voltaje RMS no es más que el valor del voltaje pico (Vpico) de la misma divido entre √2 o lo que es lo mismo 0.7071xVpico.
Entonces, si por ejemplo se tiene una onda sinusoidal de amplitud 2 Vpico, el valor del voltaje eficaz será 1.4142 Voltios.
Método gráfico
El valor eficaz o RMS utilizando el método gráfico se puede hallar con razonable precisión, mediante una cantidad considerable de valores instantáneos igualmente espaciados a lo largo de la forma de onda. Para el cálculo del valor rms de una onda sinusoidal usando este método, se puede considerar únicamente la mitad de un período o medio ciclo positivo.
Entonces, se divide esta forma de onda en "n" segmentos de tal forma que se toman las amplitudes (eje de voltajes) para cada instante de división del eje temporal. Luego, se toma la raíz cuadrada al valor resultante de sumar los valores de las amplitudes elevadas al cuadrado y dividiendo dicha suma entre los n valores. Vale mencionar que a mayor cantidad de muestras n, se obtendrá mayor exactitud en el resultado final.
Por ejemplo, considerando el siguiente gráfico de una sinusoidal de medio ciclo positivo, con amplitud de 2 Vpico.
Además, en la siguiente tabla se muestran los valores de cada valor de amplitud asociado a su fase correspondiente.
Luego, se aplican los valores tomados del gráfico en la fórmula correspondiente, tal como se muestra de la siguiente forma:
Por lo que el resultado obtenido es 1.415 Voltios, valor muy cercano al resultante mediante el método analítico.
Finalmente, se debe mencionar que en la práctica existe instrumentación capaz de medir el valor eficaz, como por ejemplo el multímetro o el osciloscopio.






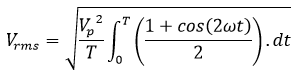













1 Comentario:
excelente resumen!��
Dejar un comentario
Los comentarios están siendo moderados y serán publicados a la brevedad.